[最も人気のある！] 等差数列の和 公式 小学生 134623

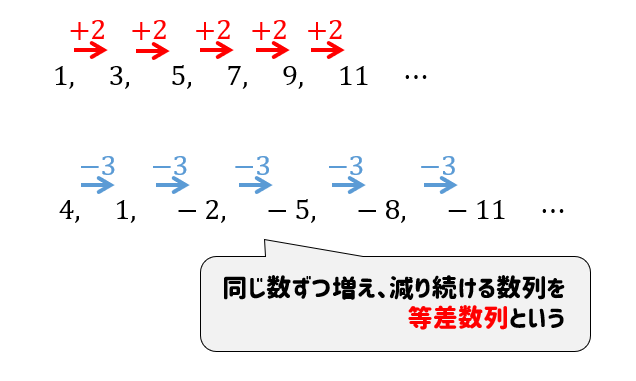
・等差数列の和を工夫して求めることを考え、一般化して和を求めることができるようにする。 (2)本時の計画 学習内容 学習活動 指導上の留意点 評価の観点 導入 (10) ・自然数の和を求める。 ・工夫して計算するように指示 する。 ・効率よく求めようとし陈金跃 等差数列求和公式的变换与意义j 中学数学研究, 02(12)4142 3 刘锡凤 等差数列求和公式的应用教学设计j 中国科教创新导刊, 13(2)9495 4 齐龙新, 王红艳 等差数列求和公式变式的灵活应用j 高中数理化, 09(2) 5 杜莹梅 等差数列求和公式的階差数列の項番号は，元の数列の 小さい方の番号 と同じです。 b n = a n1 a n b n →a n 例 次の数列において， 6＋5＝11 6＋5＋7＝18 6＋5＋7＋9＝27 6＋5＋7＋9＋11＝38 です。 ※ 高校では，Σの部分は「実際に和を表わしていること」が条件になります。

等差数列の和を計算する2つの公式 具体例で学ぶ数学

等差数列の和 公式 小学生

等差数列の和 公式 小学生-等差数列求和公式 一、等差数列 1、 Sn n(a1 2 an ) 或 Sn 2na1 n(n 2 1)d an a1 (n 1)d n N 推导过程： Sn n(a1 2 an ) = n(a1 a1 n(n 2 1)d ) = 2na1 n(n 2 1)d 性质： 若 m、n、p、q N ①若 m＋n=p＋q，则 aman=apaq ①若 mn=2q，则 aman=2aq 二、等比数列求和公式 q an (1) 等比数列： an1 n N (2) 通项公式： an a1 q(n1) 推广式： an am q(nm) (3等差数列和 一個等差數列的首 n 項之和，稱為等差数列和（sum of arithmetic sequence）或算術級數（arithmetic series），記作 S n 。 舉例來說，等差數列 {1, 3, 5, 7} 的和是 1 3 5 7 = 16 。 等差數列求和的公式如下：

中学受験の等差数列の問題を解説 等差数列の問題を解くための2つの公式

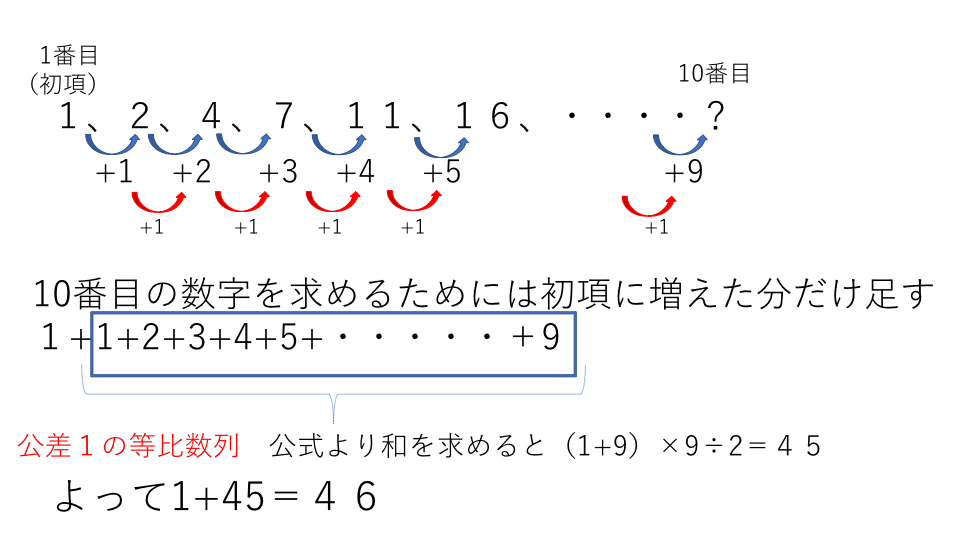
この数列は等差数列ですから，1と2で学習した公式を使えば，「 番目の奇数」 や「 番目までの奇数の和」を求めることができますね。 でも，奇数をならべた数列では，次の公式を使うと，もっとかんた前回 https//googl/LFNGHA 次回 https//googl/O1NiMG動画のプリント（19ch） http//www19chtv/サブチャンネル とある男が 「等差数列の和」を求められれば解ける問題です。 三角数の和 2問目、3問目はほぼ同じ問題ですが、「三角数の和」を求める問題です。 これ、小学生が解けるんかいな！？すげーな、中学受験生は！ とりあえず「三角数の和」をビジュアル化してみますた。

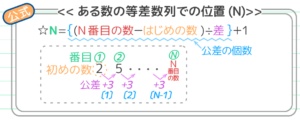
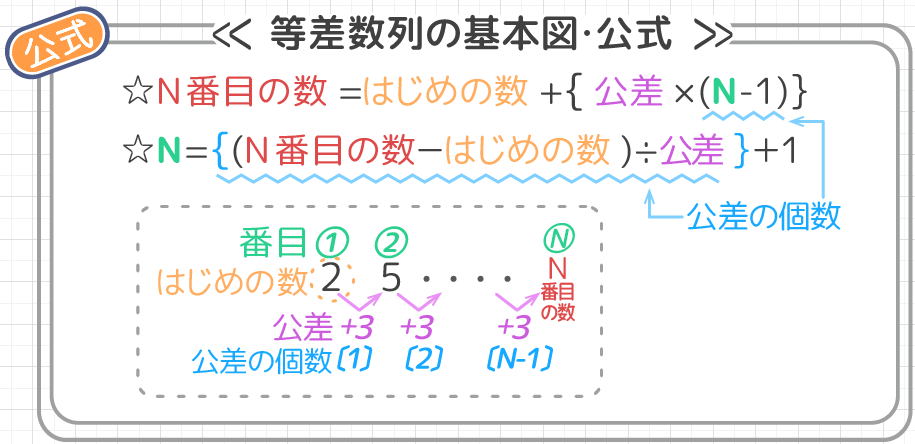
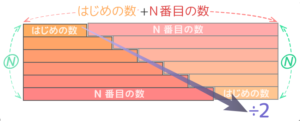
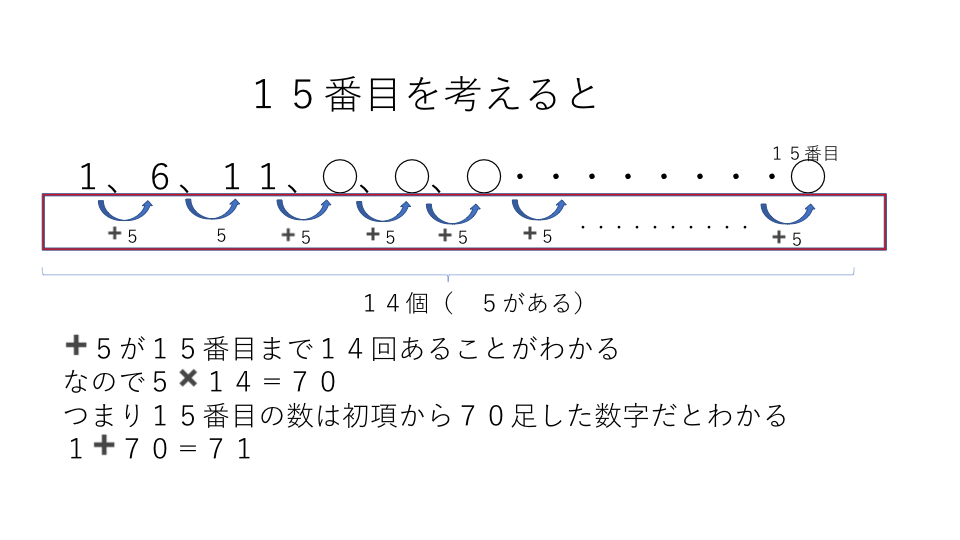
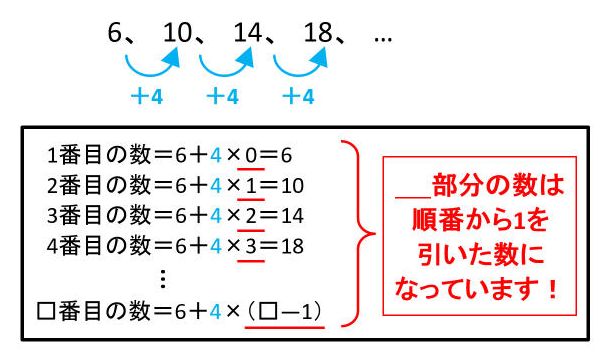
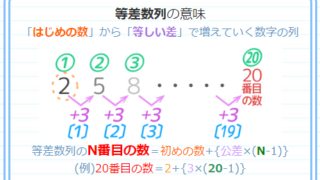
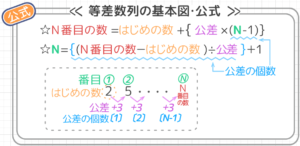
 等差数列の解き方・テクニックは公式2つ！ 番目の数＝1番目の数＋公差×（ ー1） 1番目から 番目までの数の和＝（1番目の数＋ 番目の数）× ÷2 ＊公式を忘れたら、簡単な等差数列を自分で作って数を当てはめてみると思い出しますよ 等差数列は基本問題 100番目の数が分かったので、和の公式 「等差数列の合計＝(はじめの数 ＋最後の数) 数の個数÷2」 を使って答を出します。和を求めるための練習 手を動かして公式の成り立ちを理解してみましょう。 等差数列 通常よく出る問題を作りました。 n番目はいくつか;

個数のほうが2でわり切れない場合は、数列の平均を求めて個数をかけるという考え方になります。 1から9までの数の平均は、 (1＋9)÷2＝5です。 これが個数分（＝この場合は9個）あるので、5×9＝45が1から9までの整数の和になります。算数 等差数列 等比数列 ツイート 塾講師ステーション情報局には現役塾講師に役立つ指導のコツ満載！ 小学生に数列の和の公式を理解させる方法を分かりやすく紹介！ この記事は会員限定記事です衝突判定の総当たり数の計算 10 1438 女 / 歳未満 / 学生 / 役に立たなかった / 使用目的 わが15、2乗の和がの 等差数列をなす3つの数をもとめるため。 アンケートにご協力頂き有り難うございました。 送信を完了しました。 等差数列の和

等差数列の一般項と和 おいしい数学

1

 ですので、等差数列の 番までの和の公式を使って求めることができます。 そして出てきた値に初項を足すと 1＋45＝46となります。 答え46次のような数列は等差数列ではありません。 1 , 3 , 6 , 10 , 15 , 21 , 28 , 2 , 4 , 8 , 16 , 32 , 64 , 128 , 等差数列は公式を使っていっきに和を求めることができます。 等差数列の和の公式＝(最初の数＋最後の数)×数の個数÷2 等差数列の和の公式は非常に重要な 先程の考え方を使うと、 Aの10番目の数＝Aのはじめの数＋Bの9番目までの和 です。 まず「Aのはじめの数」は 2 です。 次に「Bの9番目までの和」を求めます。 等差数列の和の公式 (はじめの数＋N番目の数) N÷2 をB1,2,3,4にあてはめると、「はじめの数」=1,「9番目の数」=9「N」=9なので 「Bの9番目までの和」＝ (1＋9) 9÷2＝ 45 になります。 以上より、 Aのはじめの数=2

中学受験の基礎知識 等差数列 後編 番までの和 Youtube

等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

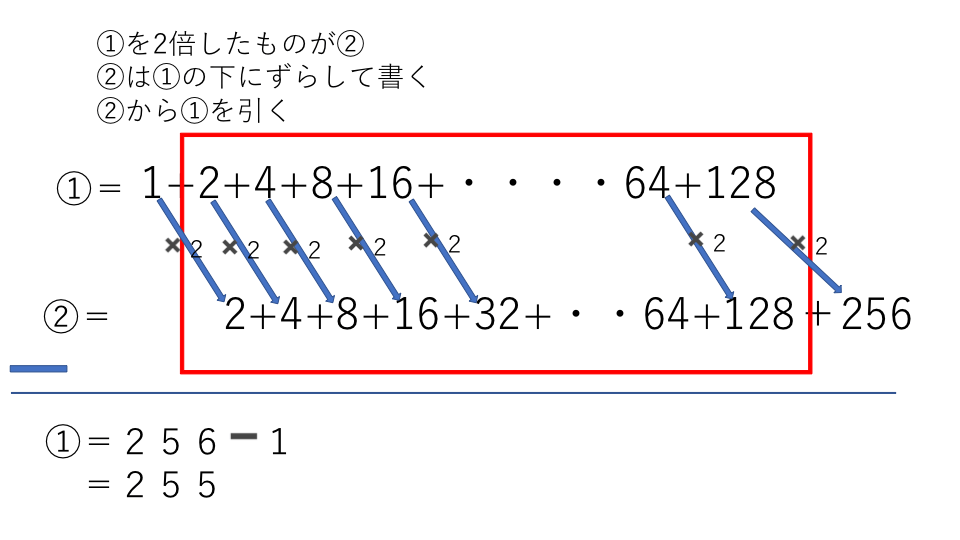
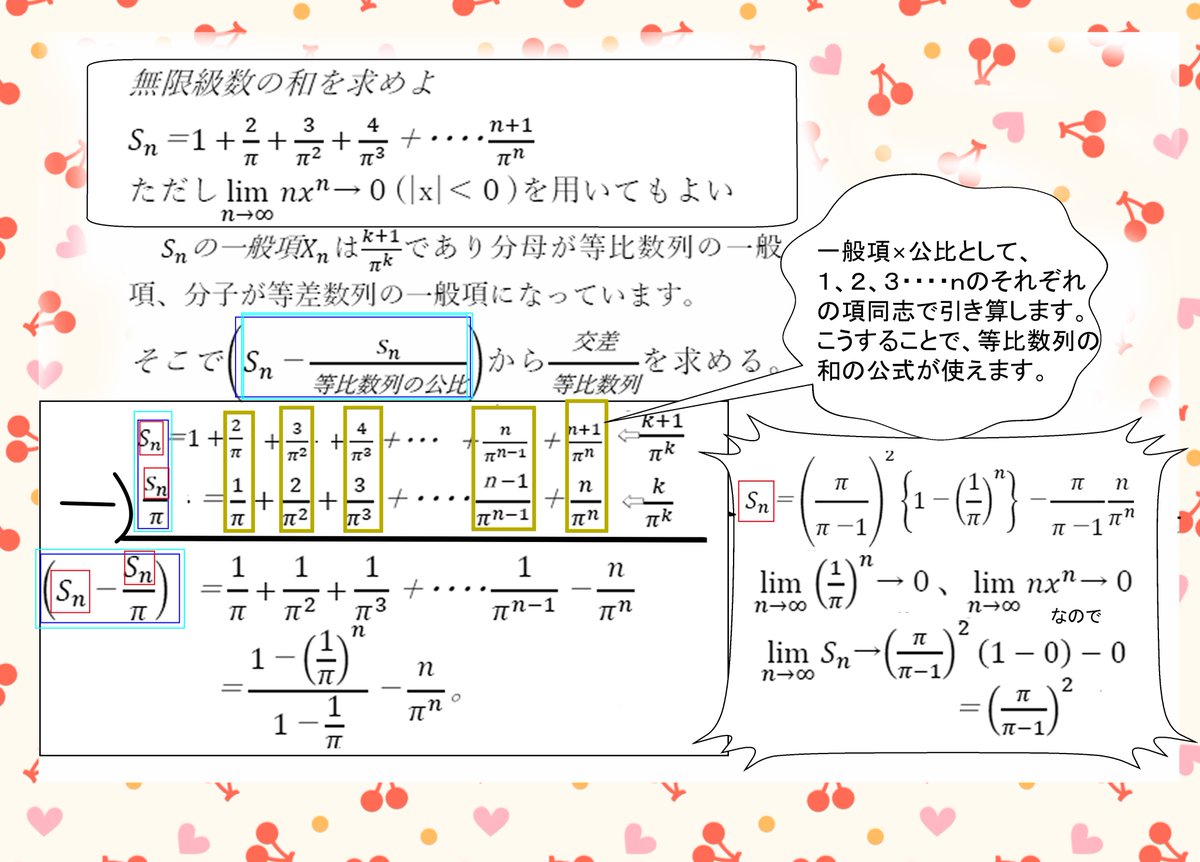
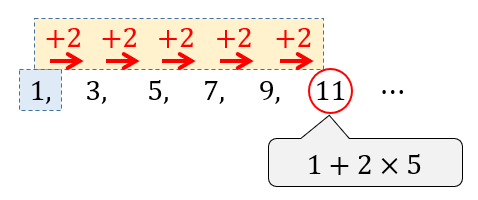
 小学生の皆さんはもちろん知らないと思いますが、高校生では等差数列というものを学びます。 ここでは、公式だけ紹介しておきます。 例えば以下のような数字の列は初項（はじめの数）1、末項（最後の数）100、項数（数字の個数）100、差 ( 前の数と次の等差数列公式 等差数列公式an=a1(n1)d 前n项和公式为Sn=na1n(n1)d/2 若公差d=1时Sn=(a1an)n/2 若mn=pq则存在aman=apaq 若mn=2p则aman=2ap 以上n均为正整数 文字翻译 第n项的值an=首项(项数1)*公差等差数列 例： 2 4 6 ⋯ 100 = 2550 246\cdots 100=2550 2 4 6 ⋯ 100 = 2550 初項が a a a ，末項が l l l ，項数が n n n であるような等差数列の和は， 1 2 n (a l) \dfrac{1}{2}n(al) 2 1 n (a l) →等差数列の和の公式の例題と証明など 等比数列 例： 1 2 4 8 16 = 31 =31 1 2 4 8 16 = 31

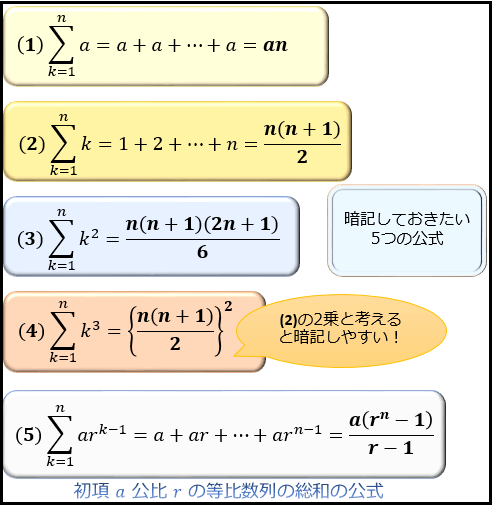
総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

中学受験 差 階差数列 を利用する問題の解き方 無料プリントあり そうちゃ式 受験算数 新1号館

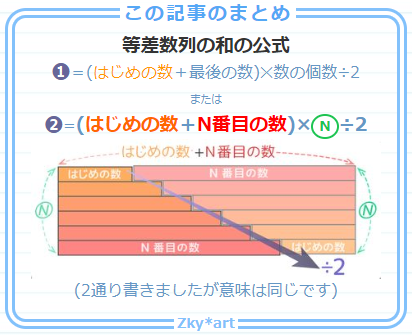
 これが等差数列の和の公式だ。 ガウス君の問題だと、 n = 100, a 1 = 1, a 100 = 100 なので、 S 100 = 1 2 100 × (1 100) = 5050 というように、公式 (2)を使えば、この問題は瞬殺できる。等差数列の和の公式導出 公式の導出 等差数列 {a n} の初項を a 1 ，公差を d とすると， a 2 = a 1 d a 3 = a 2 d = a 1 2 d a 4 = a 3 d = a 1 3 d a 5 = a 4 d = a 1 4 d , ⋅ ⋅ ⋅ よって，第 n 項は， a n = a n − 1 d = a 1 (n − 1) d また，第 n 項までの和は， S n = a 1この問題は、 「等差数列の和の公式」 を覚えていないと解くのが難しいのです。 等差数列の和の公式は、 N番目までの等差数列の和＝｛初項（初めの数）＋末項（終わりの数）｝×項数（個数）÷2

数列の誰かが小学生のときに考え出した公式についてです 確か等差数列かな Yahoo 知恵袋

数学の天才 ガウス少年 等差数列の和の公式の考え方 スモビュ

 等差数列における連続する3つの項であるa, b, cは、公差をdとすると、 a = A d b = A c = A d と表せます。 ac = A d A d = 2A = 2b よってac = 2bです。 この法則を使った問題を解いてみましょう。 問題等差数列をなす3数があり、その和は15、積は105である。よって，2S10=24×10=240 より S10=1 となります。 一般に，初項 a，公差 d，項数 n の等差数列の末項を としますと，初項から第 n 項までの和 Sn は， Sn=a (ad) (a2d) (d) (3) となります。 また，S10は上の例と同様に， Sn= (d) (2d) (ad)a (4) と書けますので， (3)と (4)の辺々加えますと，を得る。 そして等差級数の平均値 S n /n は、明らかに (a 1 a n)/2 である。 499年に、インド数学・ 天文学 （英語版） 古典期の傑物数学・天文学者であるアーリヤバタは、 Aryabhatiya （英語版） (section 218) でこのような方法を与えている。 総乗 初項 a 1 で、公差 d である総項数 n の等差数列

算数 本当に 分かる という事 等差数列その１ エース学院

等差数列の問題の解き方は 植木算や倍数の問題にも応用してみよう 中学受験ナビ

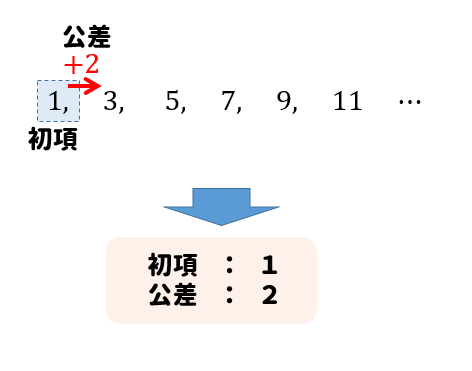
1．等差数列 むかしむかし西ドイツにガウス少年という人がいました。 ガウス少年が小学生のとき、 (9歳のときといわれているので、小学3年生ぐらいでしょうか)、ある先生が算数の授業のときに次のような宿題を出しました。 「1、2、3と自然数を 100まで足していくとその和はいくつになるか」よって、初項＋公差× (n1)　これが等差数列の一般項を求める公式になります。 例えば先ほどの数列で番目の数はというと、3＋2× (1)=41となります。 まとめると、初項をa、公差をd、nを自然数とおいて、an=a (n−1)d　となります。親子で学ぶ中学受験 数列 等差数列の和 君はガウス少年になれるか？ 年09月09日 テーマ： 中学受験算数 こんばんはー。 昼間が忙しすぎて忘れておりました。 アップロードを。 今日は等差数列の和です。

等差数列の和の公式の証明を超分かりやすく解説するよ

48s96ub7b0z5f Net Tousa Suuretsu

 等差数列のときと似たような導入でかきます。覚えなくていい「等差数列の和」 算数は得意なのに数学が苦手なひとのためのブログまず、等比数列の公式として、 こんな感じで教わってるかな？ それとも みたいな感じ？ こんな感じで覚えてると、は？2 等差数列と倍数の親密な関係 等差数列は、中学までの知識だけでほとんどの問題を解決できる、貴重な「素材」だと思う。 これを、公式を駆使して、わざわざ数列嫌いを増幅させているように感じる。 1回目の授業のテーマは、 "数を使って遊ぼう！等差数列の和 初項 a ，末項 l ，項数 n である等差数列の和 S n は， この公式は，「台形の面積の公式と同じ」と覚えるとよい．

等差数列の和の公式の例題と証明など 高校数学の美しい物語

小学生算数 等差数列 等比数列を攻略 塾講師ステーション情報局

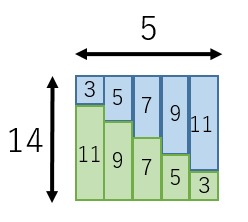
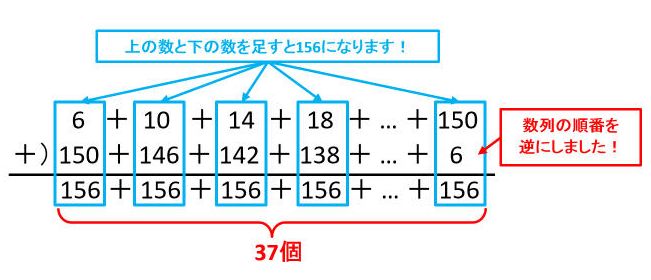
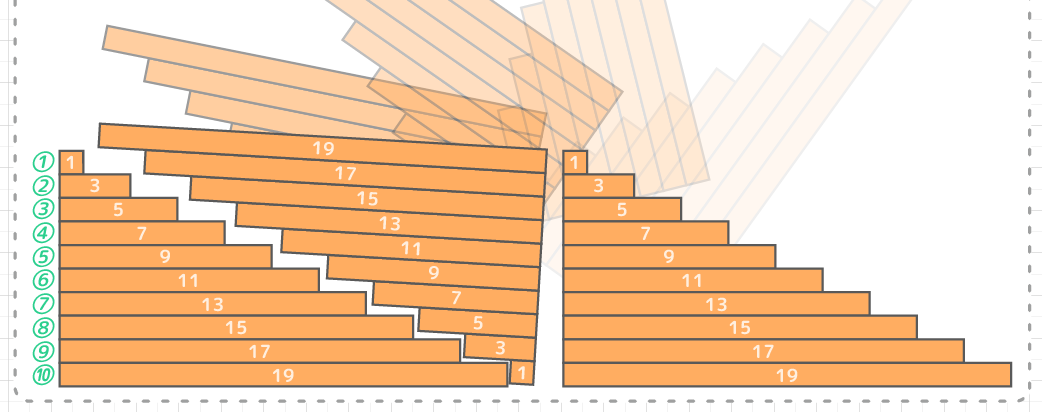
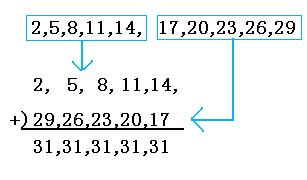
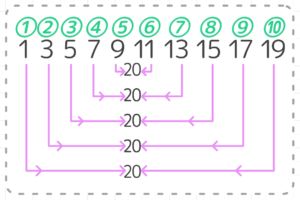
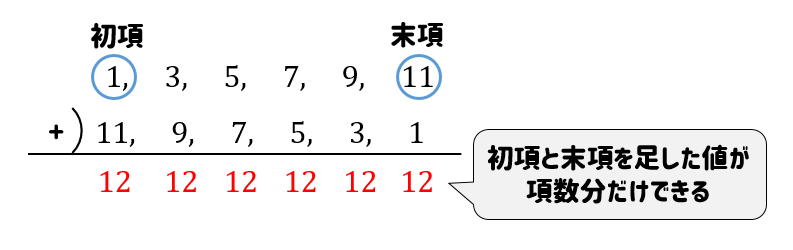
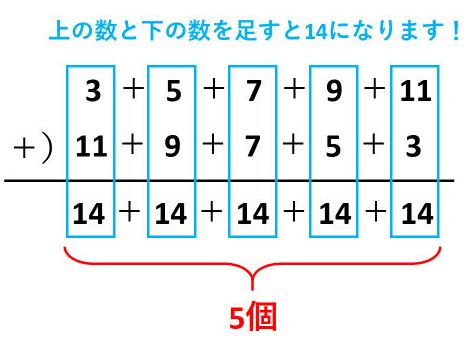
等差数列の和を求める公式を導くとき，決まって少年ガウスの 逸話を紹介する． 1から100 までの和（40 までという説もある）の計算を，逐一足 していくのではなく， (初項末項)×項数/2 で即座に答等差数列とその和 ・等差数列の隣接する項の関係を考 察し、その一般項や第n項までの和 を求めることができる。 ・一般項を表すことができたか。 ・等差数列の和の公式を理解し、そ れを適切に利用で 等差数列の和を求める場合、数列を逆順に並べるのがコツです。 3＋7＋11＋15＋19を逆順に並べると19＋15＋11＋7＋3です。 3＋7＋11＋15＋19と19＋15＋11＋7＋3を次のように足します。 数列を縦に足していくと22が5個できます。

無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

等差数列をグラフにしてみよう 父ちゃんが教えたるっ

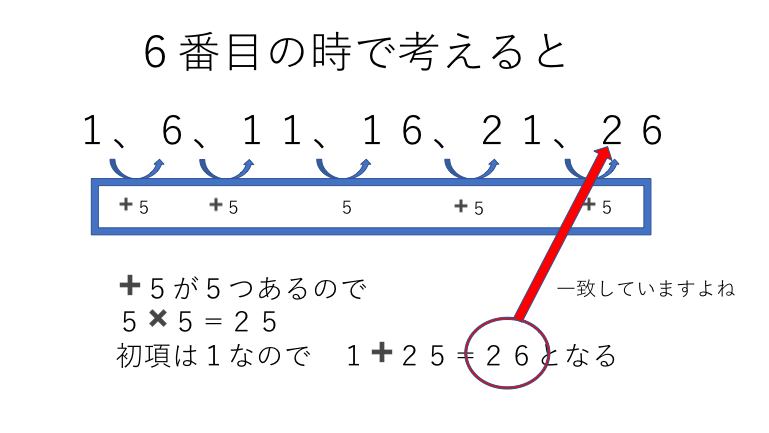
 等差数列の和（具体例） 次のような等差数列を考えてみましょう。\ 1,4,7,10,13,16,19 \これは、初項が $1$ で、公差が $3$ 、項数が $7$ の等差数列です。この数列の和を考えてみましょう。 もちろん、前から順番に足していく、という方法もあります。 算数での公式 番 目 ま で の 和 項 数 初 項 項 数 等 差 公 式 78 番 目 ま で の 和 = 項 数 × { 2 × 初 項 ( 項 数 − 1) × 等 差 } 2 公 式 = 78 × { 2 × 4 ( 78 − 1) × 6 } 2 = 130

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等差数列の和を計算する2つの公式 具体例で学ぶ数学

規則性の問題を間違えないコツ 等差数列

中学入試で出題される数列タイプのまとめ集をアップしました 恋する中高一貫校 適性検査 中高一貫校徹底攻略 小学校 算数 数学ノート 中学数学

中学受験算数 これだけ 算数のカギ 規則性 等差数列の基本 Spi Youtube

等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

3分でわかる 等差数列の公式をわかりやすく 合格サプリ

等比 等差の和を求める２通りの方法 高校数学の美しい物語

中学受験 算数 等差数列 等比数列 階差数列の重点ポイントまとめ 中学受験アンサー

無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

規則性の問題を間違えないコツ 等差数列

無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

中学受験 算数 等差数列 等比数列 階差数列の重点ポイントまとめ 中学受験アンサー

無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

数列の和 小学生でもわかる等差数列の和 東進衛星予備校 名古屋新瑞橋校のブログ

中学受験の等差数列の問題を解説 等差数列の問題を解くための2つの公式

数列の公式はどうして成り立つの N番目の数や和の求め方を本質から理解しよう 中学受験ナビ

等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

5講 等比数列の和 1節 等差数列と等比数列 問題集 3章 数列

算数 本当に 分かる という事 等差数列その２ エース学院

中学受験の等差数列の問題を解説 等差数列の問題を解くための2つの公式

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

5講 等比数列の和 1節 等差数列と等比数列 問題集 3章 数列

中学受験 数列の規則性を確実に見つける 小学生のための７つ道具 かるび勉強部屋

等差数列の和の公式の証明を超分かりやすく解説するよ

算数 本当に 分かる という事 等差数列その１ エース学院

3講 等差数列の和 1節 等差数列と等比数列 問題集 3章 数列

等差数列の公式は覚えずに 自分で15秒で作ろう

無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

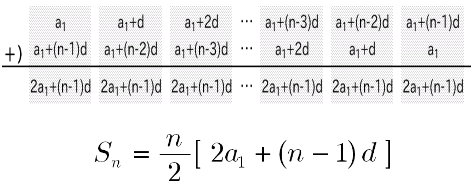
数列 等差数列の和を求める 大人が学び直す数学

中学受験算数 数列 等差数列 問題演習編 Youtube

無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

規則性 数列の基本 中学受験準備のための学習ドリル

等差数列の和 Jsciencer

等差数列

中学受験 算数 等差数列 等比数列 階差数列の重点ポイントまとめ 中学受験アンサー

等差数列の問題の解き方は 植木算や倍数の問題にも応用してみよう 中学受験ナビ

等差数列の和の公式で 写真のような公式があると思いますが これの Yahoo 知恵袋

階差数列の和 三角数 父ちゃんが教えたるっ

階差数列の和 三角数 父ちゃんが教えたるっ

階差数列とは 和の公式や一般項の求め方 漸化式の解き方 受験辞典

規則性の問題を間違えないコツ 等差数列

中学受験 算数 等差数列を極める3つのポイントと公式

1乗和 2乗和 3乗和の公式 導出法から理解しよう

等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

3

４年生向け 中学受験 算数 等差数列入門 等差数列の和の公式の使い方を例題とともに解説します Youtube

等差数列の和の公式の証明を超分かりやすく解説するよ

無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

一次関数 の新着タグ記事一覧 Note つくる つながる とどける

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

等差数列の和の公式の証明を超分かりやすく解説するよ

中学受験 算数 等差数列 等比数列 階差数列の重点ポイントまとめ 中学受験アンサー

等差数列の公式まとめ 一般項 和の公式 証明 理系ラボ

無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

等差数列の和の公式の証明を超分かりやすく解説するよ

無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

等差数列

等差数列の公式まとめ 一般項 和の求め方をイチから学んでいこう 数スタ

総和記号 S シグマの計算法と5つの公式 等差数列 等比数列を分かりやすく考えるコツ アタリマエ

数列の公式はどうして成り立つの N番目の数や和の求め方を本質から理解しよう 中学受験ナビ

等差数列の和の公式の証明を超分かりやすく解説するよ

等差数列の公式は覚えずに 自分で15秒で作ろう

等差数列 等差数列とは 中学受験の基礎知識 マスラボ Youtube

階差数列も群数列も実は解き方は1パターン 数列の練習問題 応用編

等差数列の問題の解き方は 植木算や倍数の問題にも応用してみよう 中学受験ナビ

規則性の問題を間違えないコツ 等差数列

等差数列の和 怜悧玲瓏 高校数学を天空から俯瞰する

中学受験 算数 等差数列 等比数列 階差数列の重点ポイントまとめ 中学受験アンサー

数列の基本５ 階差数列の考え方は簡単 階差数列の公式

中学受験の基礎知識 等差数列 前編 番目の数 Youtube

等差数列 公式を導いてみよう N番目の数も和も簡単に求められる ページ 2 みみずく戦略室

等差数列 数列の和を求める 中学受験の基礎知識 マスラボ Youtube

規則性の問題を間違えないコツ 等差数列

無料プリント 等差数列の和の公式の求め方と問題の解き方 中学受験 そうちゃ式 受験算数 新1号館

数学の天才 ガウス少年 等差数列の和の公式の考え方 スモビュ

高校数学b 適当に並び替えると等差数列にも等比数列にもなる3数 受験の月

みんなの算数オンライン 教科書 等差数列の和

階差数列も群数列も実は解き方は1パターン 数列の練習問題 応用編

規則性の問題を間違えないコツ 等差数列

５分間studying 数列 3 等差数列の和 数 Bを ぶっ飛ばせ

等差数列をグラフにしてみよう 父ちゃんが教えたるっ

Q Tbn And9gcsrvyyhjkytc3 8evzp90j3lssnfzqkv5ciallewoxoskrtpciu Usqp Cau

等差数列とは 和の公式や一般項の覚え方 計算問題 受験辞典

Studydoctor等差数列の和の公式 初項と公差 数ｂ Studydoctor

1